Os favoritos na estatística: Brasil, Espanha, Alemanha e França, na ordem

(*) Fábio Moraes, Márcio Pagés e Thovan Tucakov participaram da elaboração desta análise. Todos são economistas da LCA

O brasileiro analisa partidas de futebol como se estivesse na época de Charles Miller, a partir de noções como “alterações cosméticas”, “volume de jogo”, “maré de azar”, “futebol moleque” e “crescer em campo”. É engraçado e, evidentemente, tem muito valor. Difícil imaginar, por exemplo, analista de futebol melhor que o dramaturgo Nelson Rodrigues. Sem desmerecer o estilo maroto que nos caracteriza, sugiro um tour pela página “FiveThirtyEight” do americano Nate Silver para contrastar a nossa pegada com as abordagens “científicas” que dão o tom das análises esportivas que fazem mais sucesso no primeiro mundo.

Os americanos e europeus levam as estatísticas tão a sério que, em 2010, uma edição inteira do prestigioso International Journal of Forecasting foi dedicada aos esportes, com quatro artigos referentes exclusivamente ao futebol. As melhores equipes em competições de massa contam com o apoio de análises estatísticas de alto nível, seja para balizar o investimento em jogadores, seja para formular estratégias e táticas.

Os pioneiros se deram bem. O filme Moneyball conta a história do técnico de um time secundário que montou uma equipe fortemente competitiva e “barata” pedindo ajuda a um estatístico. Há alguns anos, a literatura ainda debatia a possibilidade de usar algoritmos para “bater o mercado”. Hoje, acreditamos que a maioria das frutas maduras tenha sido colhida. As técnicas são conhecidas e os dados disponíveis.

O time da LCA entrou seriamente em campo na Copa do Mundo da África do Sul, em 2010. Estimamos um modelo probabilístico baseado no diferencial entre as posições das equipes no ranking da FIFA e usamos os resultados para rodar milhares de mundiais sintéticos, observando a frequência com que as seleções levantavam a taça. O texto publicado na véspera do apito inicial chamado “Espanha parece ter mais chances do que Brasil ou Inglaterra” foi um dos maiores “best-sellers” do escritório.

Modelos para o futebol e as versões de 2010 e 2014

Prever o resultado de uma partida de futebol é arriscado porque o jogo tipicamente é decidido em poucos lances com placares miúdos, facilitando a ocorrência de zebras. O problema é menor ao prever o desfecho de um campeonato longo por pontos corridos porque a influência do acaso tende a ser diluída entre as várias partidas – “maré de azar” só existe nas mesas redondas. Em copas do mundo, no entanto, os times até conseguem reverter um tropeço na primeira fase, mas a partir das oitavas o torneio é decidido no mata-mata. Sendo assim, os imprevistos e a estrutura das chaves são fatores que podem prejudicar o melhor time, piorando as previsões.

Por melhor que seja uma seleção, dificilmente ela entra no campeonato com probabilidade de sucesso muito maior do que 25%. Por isso, qualquer palpite seco em um time tem mais chance de ser furado do que dar certo. O cenário mais provável contra qualquer alternativa não é necessariamente o melhor contra a soma delas. É curioso, mas esse fato aparentemente óbvio costuma causar confusão e explica, entre outras razões, a má fama dos economistas.

Focando a questão pelo prisma oposto, a condição de “caixinha de surpresas” não faz do futebol um jogo com desfecho aleatório. A crítica mais comum aos modelos matemáticos é a impossibilidade de prever os acidentes. É simples constatar, no entanto, que se as partidas da Copa fossem decididas no cara ou coroa qualquer time teria chance de cerca de 3% de ser campeão, o que não é razoável. Não é preciso ser expert para atribuir ao Brasil e à Alemanha probabilidades de sucesso maiores que as de Egito e Irã. Não foi por sorte que junto com os teutônicos levamos quase metade de todos os troféus.

A vantagem de um modelo matemático é olhar os times sem a influência dos preconceitos e das paixões que normalmente enviesam os comentários dos especialistas. O modelo busca padrões no passado para obter uma medida da imprevisibilidade dos jogos. Evidentemente não há fórmula capaz de prognosticar que fulano perderá a cabeça e será expulso, que o juiz dará uma forcinha para o time da casa, que o melhor goleiro do mundo engolirá um frango que o Saci Pererê evitaria e etc. Ainda assim, dá para calcular a frequência com que os jogos terminam de forma “ilógica” e usar a informação para simular a chance de zebras no futuro.

A Espanha foi de fato campeã em 2010 e o nosso modelo cravou três dos quatro semifinalistas. Os leitores interpretaram a simulação como uma aposta “seca” e, naturalmente, não fizemos o menor esforço para emendar essa apreciação quando o elenco de Vicente Del Bosque desbancou a Holanda. No entanto, a análise original destacava a baixa probabilidade de vitória de qualquer equipe individualmente e, ironicamente, uma de nossas “recomendações” era “vender” a Espanha porque os mercados pareciam superestimar suas chances de vitória. Não custa lembrar que ela foi derrotada pela medíocre Suíça logo na estreia – quem vendeu no início e zerou logo após pode ter ganhado mais do que os que adotaram uma estratégia “long only”.

As simulações sugeriam apostas contra a Argentina e Inglaterra e, em certa medida, a favor da Holanda. Em todos esses casos o modelo previu corretamente que os “preços de mercado” contrariavam os fundamentos futebolísticos. A nosso ver, o grande êxito da primeira edição foi mostrar como os analistas comeram bola em relação ao potencial do Uruguai.

Atribuíamos ao time de Diego Forlán uma probabilidade de vitória igual à da Inglaterra. O time inglês era considerado favorito ao título e as bolsas davam chance duas vezes maior para a equipe de Green, Lampard e Rooney do que para a “Celeste”. No final, o Uruguai terminou em quarto lugar e Forlán foi considerado o melhor jogador.

A versão do modelo de 2014, que incluiu pequenos aperfeiçoamentos técnicos em relação à versão de 2010, indicava o Brasil como favorito, com 20% de chance de levar o caneco. A variável incluída para capturar o “efeito casa”, que teve pouca influência no mundial da África Do Sul, foi determinante para o modelo preferir a nossa seleção.

No final, fomos atropelados pelo time alemão na maior humilhação de todos os torneios – nunca havíamos perdido por mais de dois gols em uma copa, com exceção da derrota também polêmica por 3×0 para a França na final de 1998. De qualquer forma, apesar do fiasco do time do Felipão, o modelo cravou novamente três dos quatro semifinalistas: Alemanha, Argentina e Brasil.

A estrutura da Copa da Rússia

A nova versão do modelo inclui aperfeiçoamentos, dentre os quais o uso de um indicador melhor do que o Ranking FIFA para capturar a qualidade dos times, um método para computar a probabilidade de empates de forma mais aderente à realidade e a consideração de uma variável para medir o poder ofensivo das equipes, essencial em um campeonato disputado no mata-mata.

As simulações indicam que as seleções com maior probabilidade de vitória em um confronto hipotético contra o “time médio” ou “representativo” do mundial são Brasil, Alemanha e Espanha, com chance de sucesso de cerca de dois terços. Inglaterra e México são as equipes que mais se aproximam do que o modelo considera o time representativo, com chances de vitória próximas de 50%. As estatísticas da equipe russa não são favoráveis, mas o modelo dá ao time de Vladimir Putin chance de vitória de 38% em um jogo típico quase que exclusivamente pelo “efeito casa”. Os times mais fracos são Arábia Saudita, Egito e Tunísia. A figura 1 mostra a ordenação das seleções em termos de sua chance contra o “time médio”.

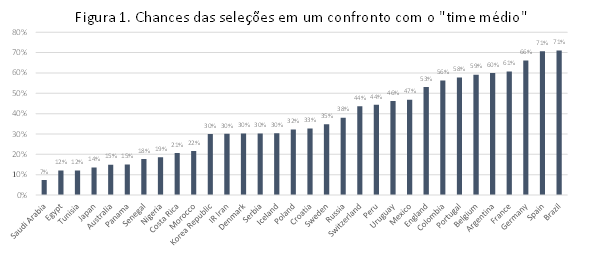
A figura 2 compara a probabilidade de vitória do “time médio” de cada grupo (excluindo cabeças-de-chave) contra o “time médio” do campeonato para medir a dificuldade dos grupos do ponto de vista do melhor time. Para fazer a comparação, consideramos Uruguai e Inglaterra como cabeças-de-chave dos grupos A e G porque o Elo médio dessas equipes é maior do que o dos líderes oficiais, Rússia e Bélgica. Sob este critério, o grupo A é o mais fraco. Uma equipe com os atributos médios de Rússia, Egito e Arábia Saudita tem apenas 16% de chance de vitória contra uma equipe representativa do campeonato – sorte do anfitrião. O grupo H também é fraco e as maiores pedreiras são os grupos B e F, que terão partidas do calibre de Espanha x Portugal e Alemanha x México. O grupo do Brasil é o terceiro mais difícil.

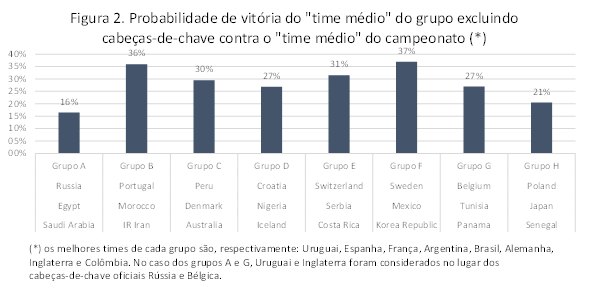
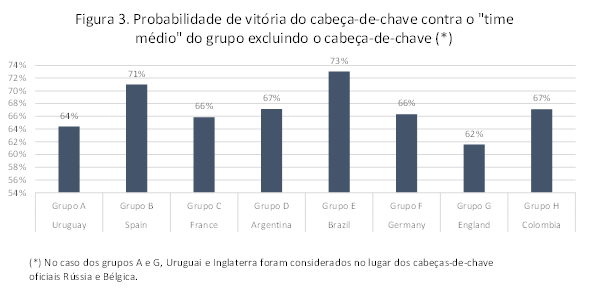
A figura 3 é parecida com a anterior e mostra a probabilidade do melhor time de cada grupo vencer uma equipe com os atributos médios dos outros três. O trabalho tende a ser relativamente mais difícil para a Inglaterra que, apesar de não estar no grupo mais difícil, tem chance maior de tropeçar no começo do campeonato por conta das próprias limitações – na verdade, projetar o fiasco inglês tem sido uma das maiores barbadas dos últimos mundiais. O inverso ocorre com a seleção brasileira. Nosso grupo é relativamente difícil, mas, façamos figas, tenderemos a “sobrar” na primeira fase por conta dos méritos do time de Tite. Ao lado da Espanha, temos mais de 70% de chance de vitória contra a equipe média do grupo respectivo.

Principais resultados e “recomendações”

A tabela mostra o Elo, ranking FIFA, resultado das simulações e “preços de mercado” extraídos de dois sites de apostas, o Bet365 e Betfair. O Brasil aparece como favorito, ligeiramente acima da Espanha, com 28% de chance de ser campeão (esse resultado depende de um detalhe metodológico referente à forma como avaliamos a efetividade do ataque das duas equipes, conforme explicação na última seção).

Curiosamente, a estrutura da chave faz com que a chance da Espanha chegar à semifinal seja um pouco maior que a do Brasil, 63% contra 61%. Como não estamos tratando aqui de uma ciência exata, o que o modelo está dizendo na verdade é que os favoritos são Brasil ou Espanha com uma probabilidade conjunta de sucesso de 60%.

As boas perspectivas da Espanha destoam de sua posição no ranking da FIFA. O modelo atribui uma chance maior para o time espanhol do que a soma das chances de Bélgica, Portugal e Argentina, que são, respectivamente, o 3º, 4º e 5º no ranking oficial. Para o modelo, se algum time levantar o caneco pela primeira vez na Copa da Rússia será a Bélgica, com um pouco mais de 5% de ser campeão. Se isso ocorrer, será uma zebra espetacular.

O modelo afirma que as chances de Brasil, Espanha e Alemanha somadas são de 71%, bem mais do que os cerca de 50% atribuídos pelas casas de apostas. Olhando o mercado, operações contra França, Argentina e, para variar, Inglaterra parecem fazer sentido.

Definindo o risco de “zebra” como o sucesso de uma seleção que não seja Brasil, Espanha, Alemanha, França e Argentina, o modelo é bem mais agressivo do que o mercado ao descartar os eventos em que nenhum desses times é campeão. Para o modelo, o imprevisível ocorre com 17%. Para o mercado, ele vem com chance duas vezes maior. Será torcida?

As seminais mais prováveis são Espanha x Alemanha (em 23.5% das simulações) e Brasil x França (em 18.4% das simulações). Brasil x Portugal, Argentina x Alemanha e Espanha x Colômbia também são semifinais que aparecem com frequência alta. Os times colombiano e belga são os “azarões” que podem chegar mais longe segundo o modelo. O time belga pode ser um osso duro para o Brasil nas quartas. Portugal também pode surpreender.

Se der a lógica, a campanha do Brasil será: México nas oitavas, Bélgica nas quartas, França na semifinal e Espanha na final.

Aspectos metodológicos do modelo

Essa seção é destinada a apresentar sucintamente a estrutura do modelo e hipóteses para simular os mundiais. Fazemos das tripas coração para expor os detalhes de forma intuitiva de modo a tornar o texto acessível à maioria. Dito isso, esta seção tende a ser relativamente indigesta aos leitores que não têm alguma familiaridade com métodos quantitativos.

O modelo foi estimado a partir de uma amostra de cerca de 3000 jogos entre seleções desde o último mundial, extraída de um universo de aproximadamente 4500 partidas. A escolha obedeceu aos seguintes critérios: (i) inclusão de todos os jogos oficiais (torneios continentais e partidas eliminatórias); e exclusão dos seguintes amistosos: (ii) que envolveram seleções com menos de 10 jogos; (iii) em que a diferença entre as posições no ranking FIFA das seleções era superior a 100 e (iv) que resultaram goleadas com mais de cinco gols. O objetivo das exclusões foi o de não enviesar as estimativas com resultados pouco representativos em relação ao grau de competitividade que se espera de um mundial.

O modelo para determinar a probabilidade de vitória do time X em um encontro com o time Y tem estrutura parecida com o usado nas edições de 2010 e 2014, incluindo as seguintes variáveis: (i) a diferença entre o “Elo rating” das seleções; (ii) uma variável binária para capturar o “fator casa”; (iii) a média de gols marcados pelos times nos 12 meses que antecederam a partida; (iv) constantes para medir a influência de variáveis que determinam a tradição dos times e; (v) variáveis para medir a maior competitividade relativa nas ligas europeia e sul-americana.

Ao invés do ranking FIFA, preferimos utilizar dessa vez o “Elo rating” dos times no momento da partida, doravante apenas Elo. Trata-se de sistema desenvolvido por um físico de origem húngara para inferir de forma rápida a “habilidade” de enxadristas. O conceito pode ser aplicado em qualquer jogo de soma zero como é o caso do futebol. A Wikipédia contém uma boa explicação para quem tiver interesse, especialmente na versão em inglês. Preferimos o Elo porque ele é atualizado jogo a jogo e produziu modelos mais aderentes. O ranking FIFA muda a cada mês e a própria entidade, preocupada com riscos de manipulação, estuda mudar a fórmula.

O sistema Elo parte do princípio natural de que a qualidade de um competidor é revelada pelo desempenho nos confrontos contra os demais. A parametrização é feita agregando pontos aos vitoriosos e subtraindo dos perdedores em uma métrica que permite inferir rapidamente a probabilidade de vitória comparando a diferença entre os escores. O modelo, na verdade, calibra com base na realidade quão adequadamente a diferença de Elo se traduz em chance de vitória, condicionando o ajuste às outras variáveis (gols, casa, liga e tradição).

Como a maioria dos jogos da amostra usada para estimar os coeficientes do modelo ocorreu dentro das ligas e não entre as ligas, é possível que haja times europeus com Elo parecido ao de times asiáticos e, evidentemente, o melhor time europeu é muito melhor do que o melhor time asiático. Essa é a razão que exigiu a inclusão de variáveis para capturar os graus distintos de competitividade entre as ligas mais e menos tradicionais.

As simulações indicam que uma seleção da UEFA tem vantagem de 2,4 pontos percentuais em relação a um adversário igual nos outros quesitos que não pertença à CONMEBOL e de 1,6 ponto percentual se pertencer. Um time da liga sul-americana, por sua vez, tem vantagem de 0,8 ponto percentual contra uma seleção das demais ligas. Os números parecem irrelevantes, mas é preciso lembrar que eles se somam aos efeitos das demais variáveis.

O maior aperfeiçoamento em relação às versões anteriores ocorreu na determinação da probabilidade de empate. Normalmente, a soma das chances de vitória de X contra Y e de Y contra X é menor do que 100, inferindo-se a partir da diferença a probabilidade de empate – as versões passadas partiram desse critério. No entanto, quando a probabilidade de empate é estimada explicitamente com as mesmas variáveis usadas para avaliar a chance de vitória, verifica-se que o resultado implícito tende a superestimar a probabilidade real quando os times possuem Elos próximos e a subestimar quando as diferenças são mais relevantes.

Para atenuar essa distorção, decidimos chegar às probabilidades de vitória, derrota e empate procedendo a uma normalização que levou em consideração a frequência de empates efetivamente observada nos últimos quatro anos, garantindo assim uma distribuição teórica mais próxima da real. Por exemplo, se o modelo prevê que o time X ganhará com 50% de chance, o time Y com 30% e houve 10% de empates nos últimos quatro anos, a simulação final será rodada atribuindo-se, respectivamente, as probabilidades de 56%, 33% e 11%. Se ao invés disso, o modelo prevê que X e Y ganharão com 30%, ao invés de supor que a chance de empate é de 40%, trabalhamos com 43%, 43% e 14%.

Para solucionar os casos em que a classificação dos times depende do saldo de gols, estimamos um modelo com estrutura semelhante ao que visa chegar às probabilidades de vitória para explicar a diferença de gols marcados por X e Y. Para manter as simulações próximas do mundo real, o modelo final foi programado para determinar o saldo de gols do time vencedor a partir do valor previsto pela fórmula normalizado para a média efetivamente observada nos últimos quatro anos de cerca de 3 gols por partida no caso dela terminar de acordo com a lógica. No caso de zebra, arbitramos o resultado em 1 a 0 a favor do azarão, supondo implicitamente que ele ganhou por conta de um lance fortuito.

Como nas versões anteriores, as probabilidades são obtidas por meio de 30.000 simulações levando em conta a estrutura dada pela chave do torneio. Os modelos foram estimados a partir do Elo no momento das partidas, mas as simulações foram geradas a partir do Elo médio. O uso dos Elos recentes poderia subestimar o potencial de equipes que após a classificação experimentam jogadores, formações distintas e tendem a “esconder o jogo” contra os rivais mais importantes.

Além das simulações que consideram a média de gols efetivamente registrada pelas equipes, rodamos também uma versão que trunca as grandes goleadas, ajustando o número de gols marcados como sendo o valor mínimo entre o efetivo e quatro. Evidentemente, esse critério deprime a média de gols dos times com ataques mais eficazes. A escolha foi feita para atenuar a forte assimetria positiva na distribuição de gols registrados por algumas seleções. Os resultados reportados abaixo correspondem à média entre as simulações com e sem esse ajuste.

A lógica é, por um lado, não penalizar os times com os ataques mais produtivos, mas levar em conta que as equipes tendem a jogar mais conservadoramente em Copas do Mundo, procurando explorar os contra-ataques após abrirem o placar e, com a vitória garantida, realizando substituições para poupar titulares e entrosar reservas.

Corrigir a assimetria dos gols marcados antes do mundial (especialmente em amistosos com times menos expressivos) é um ajuste que consideramos necessário, mas cuja programação envolve uma dose de arbitrariedade. Os efeitos práticos não são muito significativos, exceto por um ligeiro rebaixamento das chances da Espanha. Aqueles que acharem que a força do ataque espanhol no mundial deve ser medida por um índice que leve em conta goleadas como, por exemplo, os 8×0 do massacre contra Liechtenstein, devem elevar ligeiramente as chances de La Roja.